Part 2: Full SEM, with mediation and moderation

Day 3: Full Structural Equation Modeling

Two researchers are interested in burnout among academics. They have obtained the data (file: Ex2sim.dat) from 300 academics on the following variables:

The researchers want to investigate whether the detrimental effect of Emotional Exhaustion on Academic Achievement is mediated by Cynicism. They also want to control for differences between men and women in Emotional Exhaustion, Cynicism, and Academic Achievement. Hence, they propose the following model:

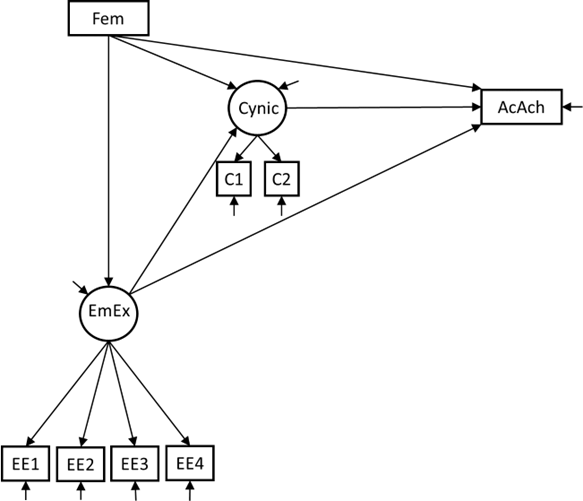
Note that, even though Fem is a categorical variable (with scores 0 or 1), we do not have to treat it differently in Mplus than the continuous variables because:

  1. It is an exogenous variable (meaning it serves as a predictor only in the model), and
  2. it is dummy variable (meaning it is a special categorical variable).

Exercise 1

Specify this model and discuss the model fit.

See the input file for Model 1. The \(\chi^{2}\) test indicate that the model does not fit, \(\chi^{2} (16) = 33.06\), \(p = .0073\). Other measures indicate acceptable model fit: RMSEA is 0.06, CFI is 0.96, TLI is 0.93, and SRMR is 0.04.

Exercise 2

Investigate whether there is an indirect (mediated) effect of Emotional Exhaustion on Academic Achievement. Remember to use the MODEL INDIRECT command, and combine this with bootstrapping and confidence intervals (see slides).

See the Ex2Model2.out file. To interpret the size of a (significant) effect, it is helpful to use the standardized results. When looking at the p-values for the standardized (bootstrap) results, we find:

  • Total effect is significant: -0.152 (SE = 0.067, \(p = .023\))
  • Indirect effect is not significant: -0.071 (SE = 0.038, \(p = .058\))
  • Direct effect is not significant: -0.081 (SE = 0.068, \(p = .234\))

Note that the total effect is the sum of the indirect and the direct effects: \(-0.152 = (-0.071) + (-0.081)\). The results here show that, while we do not have the power to detect a direct or an indirect effect, the total effect is significant.

The 95% confidence intervals for the standardized effects are:

  • Total effect (-0.283,-0.021); does not contain zero
  • Indirect effect (-0.145,0.002); contains zero
  • Direct effect (-0.213,0.052); contains zero

Hence, the conclusions based on the confidence intervals are the same as the conclusions based on the p-values.

Exercise 3

Do the same for the effect of being female on academic achievement.

Moving to the confidence intervals for standardized parameters right away, we find:

  • Total effect is -0.020, 95% CI [-0.131, 0.090]; contains zero
  • Indirect effect FEM \(\rightarrow\) Cynicism \(\rightarrow\) AcAch is 0.038, 95% CI [-0.014, 0.091]; contains zero
  • Indirect effect FEM \(\rightarrow\) EMEX \(\rightarrow\) AcAch is -0.013, 95% CI [-0.038, 0.013]; contains zero
  • Indirect effect FEM \(\rightarrow\) EMEX \(\rightarrow\) Cynicism \(\rightarrow\) AcAch is -0.011, 95% CI [-0.028, 0.005]; contains zero
  • Direct effect is -0.035, 95% CI [-0.153,0.084]; contains zero.

Conclusion: there is no evidence that being female has a direct or indirect effect on academic achievement.

Exercise 4

The researchers are also interested in investigating whether there is an interaction between being female and emotional exhaustion on cynicism; specifically, they want to know whether the effect of emotional exhaustion on cynicism is stronger for males than for females. The model they want to specify for this is visualized below:

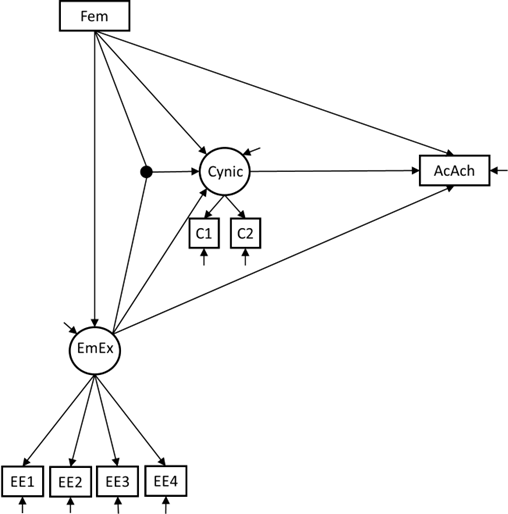
Remember that to specify an interaction between an observed and a latent variable (indicated here by the black dot) in Mplus, you need to use the XWITH statement in the MODEL command. The use of this statement requires you to use (see slides):

ANALYSIS:   TYPE = RANDOM; 
            ALGORITHM = INTEGRATION;

Note that this cannot be combined with bootstrapping, or the MODEL INDIRECT command (you get error messages when you try to do this). The latter does not imply there are no indirect effects in the model; it merely implies you cannot get the additional output for this.

Specify this model in Mplus.

See the iput file for Model 3. The interaction is specified as:

EExF | EmEx XWITH Fem;      ! Interaction

This model gives

CYNICISM   ON
    EMEX               0.343      0.105      3.263      0.001
    EEXF              -0.319      0.135     -2.361      0.018

which implies that the interaction is significant. Substantively, it implies that:

  • The effect of Emotional Exhaustion for males (Fem = 0) is 0.343, SE = 0.105, \(p < .001\).
  • The effect of Emotional Exhaustion for females (Fem = 1) is 0.319 lower than for men, SE = 0.135, \(p = .018\).

Exercise 5

We now have a slope for males and a difference in slopes between males and females. If instead, we are interested in the actual slope of females, we can ask Mplus to compute this as an additional statistic using the MODEL CONSTRAINT command. To this end, we first need to name the slopes of interest, using

Cynicism ON EmEx Fem EExF (slopeM interDiff slopeDiff);

and subsequently we can use these names to compute new statistic, using

MODEL CONSTRAINT:
      new(slopeF);
      slopeF = slopeM + slopeDiff;

This way we will obtain the estimate for the slope of females, including its standard error and p-value.

Specify this model in Mplus, and report the results.

See the input file for Model 4. The slope for females (when regressing cynicism on emotional exhaustion is not significantly different from zero:

New/Additional Parameters
    SLOPEF             0.024      0.103      0.233      0.816

Hence, we can conclude that, while for males emotional exhaustion is a positive predictor of cynicism (suggesting that more emotional exhaustion leads to higher levels of cynicism), for females, no such relation was found.